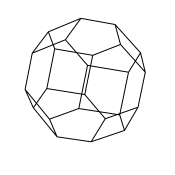
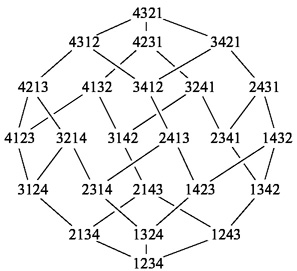
The permutahedron for n=4
I drew some pictures of a sphere divided into fundamental chambers by
hyperplanes. This was drawn using MuPad and made into a sequence
of pdf images that animate to rotate the sphere. The final images
have the midpoints of the fundamental chambers connected so that the
permutahedron appears.
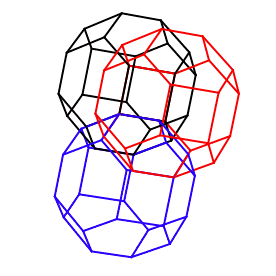
More permutahedrons on the sphere.
Permutahedrons can tile n-space.
Here is an attempt at drawing this phenomenon in 3-space.
These images were taken from a paper by Marcelo Aguiar and Frank
Sottile: Structure
of the Malvenuto-Reutenauer Hopf algebra of permutations. I
have
modified them so that they can easily be printed, copied, and used for
web applications. The gif versions of these pictures have an
invisible
background and so can be placed over other images. I needed it
because
I drew it several dozen times trying to see patterns in a problem
related
to this poset and all I wanted was a copy that I could color in.
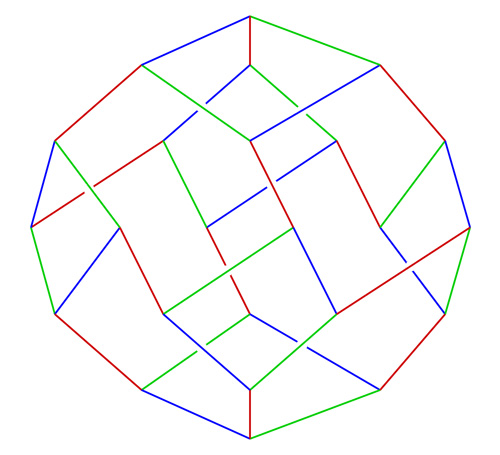 |
Click on the following links for a larger image
Color: gif jpeg
eps pdf
|
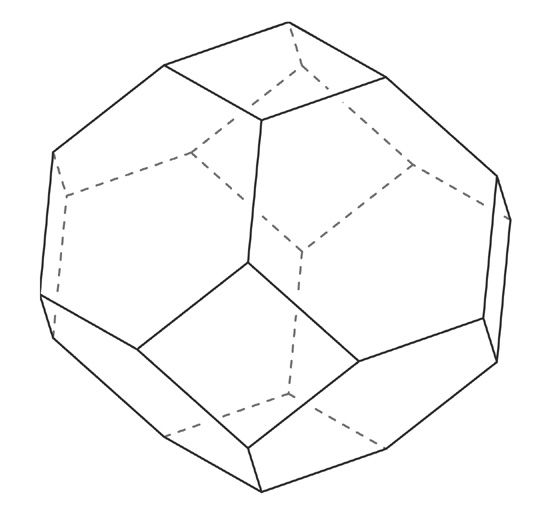 |
Click on the following links for a larger image
B&W: jpeg gif eps
pdf
|

|
|
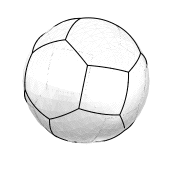
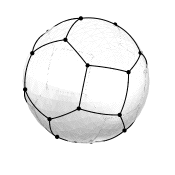
Pentagons and hexagons vs. squares and hexagons
|
|