BACK TO:

Definitions of Symbols used in this Website

An excellent general reference (and essentially the bible for research in this area) for symmetric functions is the book Symmetric Functions and Hall Polynomials by I.G. Macdonald, Oxford Science Publications, Second Edition 1995. There are other references for symmetric functions, Segan

A partiton, , is a non-increasing sequence of non-negative integers. A partition of n means that the entries in the partion sum to n. In the following definitions, and are always partitions of n. The length of the partiton is the number of non-zero entries and will be denoted by .
represents the function that is 1 if and 0 otherwise.
The arm of a cell s=(i,j) is is the number of cells that are strictly east of s and still in the diagram of . The leg of a cell s, , will be the number of cells north of s that are still in the diagram.
The co-arm and co-leg of the cell are one less than the x and y coordinates respectively. They will be denoted by and .
There is a statistic on partitions that is useful:
is the symmetric function involution that sends to .

are the Schur symmetric functions

are the homogeneous symmetric functions

are the power symmetric functions

are the elementary symmetric functions

are the monomial symmetric functions

Define an inner product

by the values on the power symmetric functions by

. This is the standard inner product on symmetric functions.

The Schur symmetric functions have the property that they are upper triangularly related to the monomial symmetric functions and orthogonal with respect to the inner product.

Define an inner product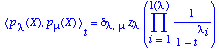

by the values on the power symmetric functions by definition of Hall-Littlewood scalar product

. This is usually referred to as the Hall-Littlewood scalar product.

Define the symmetric functions to be the symmetric functions with the property . These are the dual-Schur symmetric functions.

Define another inner product

by the values on the power symmetric functions by

definition of Macdonald SF inner product

This is the Macadonald inner product or the q,t-inner product.

The Macdonald symmetric functions Pmu(X,q,t) are defined by the property that they are upper triangularly related to the monomial symmetric functions and orthogonal with respect to the

inner product. That is, they satisfy the following two conditions

where the sum is over smaller than in dominance order.
if .

Let

where

has the expansion sum where the sum is over all partitions of n and this is the defintion of the q,t-Kostka coefficients, . The are usually referred to as the integral form of the Macdonald symmetric functions.

Define

to be another class of symmetric functions. I find that these are slighly easier to work with than the

Define the basis

as a transformed basis for the

symmetric functions. This basis is important because it is conjectured to be the Frobenius characteristic of the n! conjecture module. The corresponding transformed coefficients will be defined as

The Hall-Littlewood symmetric functions that appear here are transformed from the standard symmetric functions. They are given by the formula

where the first sum is over 1 ¾ i < j ¾ n and the second sum is over all j and 1 ¾ i ¾ n. The are analogous to the

(in fact equal when q = 0) but are a transformation of the symmetric functions normally referred to as Hall-Littlewood polynomials. The transition coefficients with the Schur symmetric basis are the t-Kostka coefficients.

Occasionally, plethystic notation is used for symmetric functions here. This is a notational device for expressing the substitution of the monomials of one expression, $E = E(t_1, t_2, t_3, \ldots)$ for the variables of a symmetric function, $P$. The result will be denoted by $P[E]$ and represents the expression found by expanding $P$ in terms of the power symmetric functions and then substituting for $p_k$ the expression $E(t_1^k, t_2^k, t_3^k, \ldots)$.

More precisely, if the power sum expansion of the symmetric function $P$ is given by $$P = \sum_\la c_\la p_\la$$ then the $P[E]$ is given by the formula $$P[E] = \sum_\la c_\la p_\la \coeff_{p_k \rightarrow E(t_1^k, t_2^k, t_3^k, \ldots)}$$.

To express a symmetric function in a single set of variables $x_1, x_2, \ldots, x_n$, let $X_n = x_1 + x_2 + \cdots + x_n$. The expression $P[X_n]$ represents the symmetric function $P$ evaluated at the variables $x_1, x_2, \ldots, x_n$ since

$$P(x_1, x_2, \ldots, x_n) = \sum_\la c_\la p_\la \coeff_{p_k \rightarrow x_1^k + x_2^k + \cdots + x_n^k} = P[X_n]$$