HOME:

Here are 4 q,t analogs that are related to Macdonald polynomials and Diagonal Harmonics

Open problem:  Find a combinatorial interpretation for ANY of the q,t analogs of the known sequences listed below

Open problem: Prove that ANY of the q,t analogs of the sequences listed below are polynomials with non-negative integer coefficients (the polynomiality has already been settled, but new proofs are always welcome).

Maple programs exist on this web site if you would like to compute and experiment with these q,t-polynomials (see nabla.html).

 

the number of rooted forests on n labeled verticies

the Catalan numbers

 

the number of standard tableaux  of shape lambda

 

the multinomial coefficient

These are not the only q,t-analogs that arise from the Macdonald polynomials.  Since we have the number of standard tableaux and the binomial coefficients we may derive many sequences that have formulas in terms of these.  These may or may not have interesting combinatorial interpretations, but but since they are special cases it might be easier to find a method to attack them.

The following list is not exhaustive, but it gives an idea for different ways of looking at these q,t-analogs.
 
 

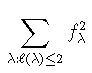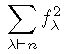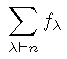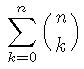	the Catalan numbers
	n!
	the number of involutions in Sn
	the Motzkin numbers
	2n