Research project on Dyck Paths
A Dyck path is a lattice path in the nxn square which
does not pass below the diagonal.
Dyck paths are one of
the fundamental objects enumerated by the
Catalan numbers.
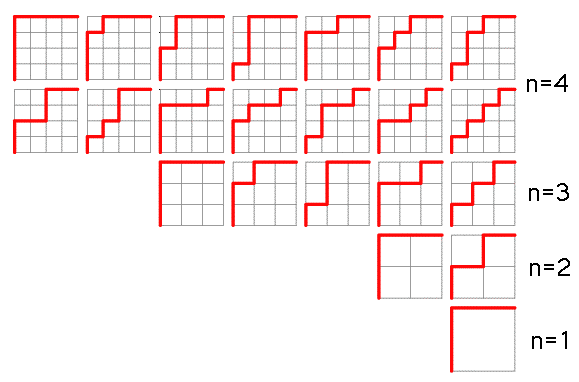
Consider the partial order of Dyck paths where one
path is 'less' than another if it lies below.
What are the properties of this poset? (it is a graded lattice where
the rank function is the area, the generating function is a q-Catalan number, can
we say more?)
Can you calculate its mobius function? What is the relationship
of this order to other
Catalan enumerated objects.
In summer of 2008 I gave this problem to a student, Jennifer Woodcock,
in the M.A. for Teachers program and she produced
the following manuscript.
This page was last edited November 16, 2008.
