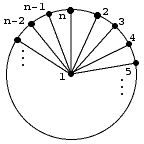
Problem #4 - How many spanning trees are there of the wheel graph for n >=
4?
This as it turns out is a hard problem, however it is not impossible and
I would like to see if there are people in this class that are resourceful
enough to solve it. I will make this a bonus problem on the homework
and it will not be graded. However if you wish to try the problem there
are two possible approaches that I think might work.
The first is to find a recurrence on the number of spanning trees of W_n
with n vertices in terms of the spanning trees of W_{n-1} and W_{n-2}. The
way I would recommend that you try this is to look at the number of spanning
trees that do not include the last vertex in the picture below and then the
last vertex must have an edge either to the center vertex, or to vertex 2
or to vertex n-1. This isn't the complete story, but it is a start.
Once you have the recurrence, solving it is a much more difficult problem,
but then perhaps you can use other tools to help you guess the answer.
The other approach I would use is to count the number of spanning trees that
have k edges on the outside wheel where 0 <= k <= n-2 (since there
must be at least one edge to the center vertex). This might be hard,
but I was able to use it to get the first 3 values (BTW, the first one must
be 16 since W_4 is the complete graph on 4 vertices). If S_{n,k} are
the number of spanning trees of W_n with k edges around the outside and n-k-1
edges from the center vertex then the total number of spanning trees will
be S_{n,0} + S_{n,1} + .... + S_{n,n-2}.
Back to the Math 3260 page