The permutahedron for n=5

These images were created by generating postscript through Maple. They represent the left-weak order on permutations, that is, two permutations are connected with a line if they are related by a transposition of 12, 23, 34, or 45. The rows a determined by the length of the permutation and the horizontal position is determined by sorting the permutation in reverse lex order. This minimizes the number of crossings in a natural way but it may be possible to do better.

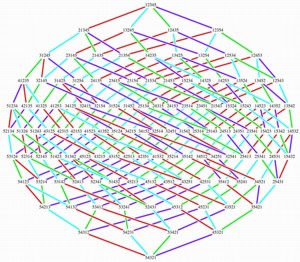
Color: jpeg gif eps pdf
B&W: jpeg gif eps pdf

These images were created in Maple. I prefer the postscript file because of the scaling problems that one has with the jpeg version, but these may be useful. The pdf version is on one page and is useful for printing, but the image is very small when scaled down to the 8 inch width. I would like to embed this poset into a sphere so that it is planar on the globe (as was done for n=4) but I am pretty sure that this is not possible.

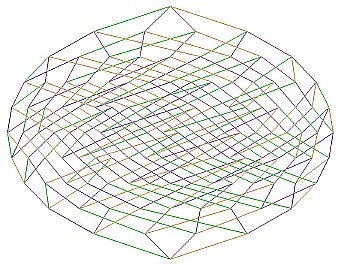Click on the following links for larger image
Color jpeg
B&W jpeg

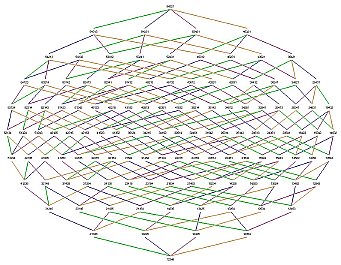Click on the following links for a larger image
Color: jpeg pdf
B&W: jpeg pdf