HOME:
BACK:	More qt-analogs

This combinatoral statistic was announced at the conference in honor of the anniversary of LaCIM at UQÀM, September 7, 2000 by Adriano Garsia and Jim Haglund.  It is the first proof of the postivity of the qt-Catalan numbers.

The combinatorial interpretation is given in terms of Dyck paths (lattice paths in an nxn square which remain above the diagonal) such that the q,t-Catalan numbers are given as the sum over all Dyck paths D, q to the power of a(D), t to the power of b(D) where a(D) and b(D) are some numbers associated to each Dyck path.

The first statistic, a(D) is well known and is the number of cells below the path and above the diagonal.

The second statistic, b(D),  is not quite so well known but has been shown to be equivalent to a statistic that is in the literature.  For every path D, there is a 'support path,' which is found by
starting in a corner of the path, moving left until one hits the path D, moving down until one hits the diagonal, moving left until hitting D, down until one hits the diagonal...until the end of the path is reached.  The statistic b(D) is given as the sum over i, where i is the position of the corners where the support path hits the diagonal.  (This is made more precise by the example below).

Here is an example:  Let D be the Dyck path

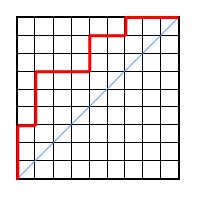There are 19 cells below the path and above the diagonal, hence a(D) = 19.
 
 

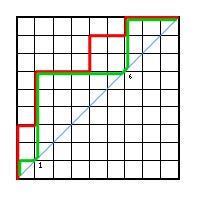The path in green is the corresponding 'support path.'  It touches the diagonal at position 1 and 6, hence b(D) = 7.

As another example we use this combinatoral interpretation to calculate the fourth qt-Catalan number.  The Dyck paths are given in red, the support paths are given in green.  The a and b statistics appear below each of the diagrams
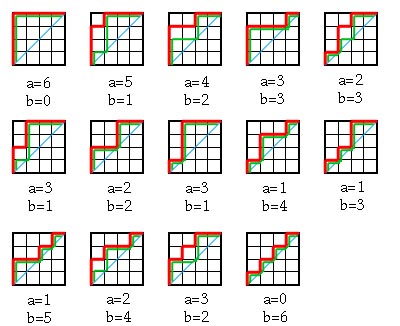
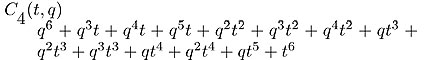