HOME:
BACK:	More qt-analogs

The (q,t)-Catalan sequence is defined by setting
 
 

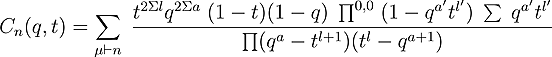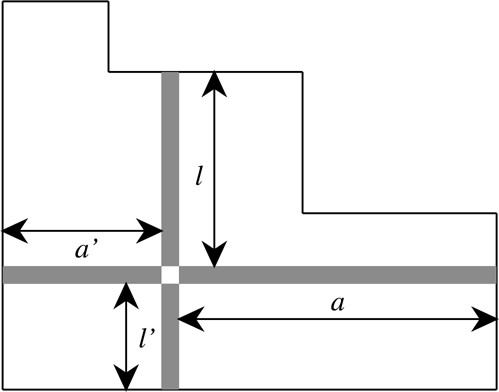
where the sum is over all partitions of n. All products and sums in the µ^th summand are over the cells of µ and the parameters l, l', a, a' denote the leg, coleg, arm and coarm of agiven cell. That is, for a given cell s, when µ is depicted bythe French convention (see the figure below) l, l',a,a' give the number of cells that are strictly north, south, east andwest of s in µ. The symbol  is used to express that this product omits the corner cell with l'=a'=0.
 
 

On the surface this formula appears to define only a rational function of q and t. Nevertheless, computer data and representation theoretical
considerations lead us to conjecture that C_n(q,t) evaluates for all n to a polynomial with non-negative integer coefficients and total degree . In fact, a perusal of the tables in the appendix quickly reveals that the coefficients of the resulting polynomial always add up to the familiar Catalan number
 
 

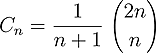By specializing the values of q and t in the (q,t)-Catalan numbers one also recovers the q-Catalan numbers.

The q, t-Catalan numbers arise naturally in the study of diagonal harmonics.  They are conjectured to be the coefficient of the sign representation in the Frobenius series for the diagonal harmonics.

The (q,t)-Catalan numbers are now known to be polynomials in q and t and there exists a proof in the article
Identities and Postitivity Conjectures for some remarkable Operators in the Theory of Symmetric Functions (to appear), François Bergeron, A. Garsia, M. Haiman, G. Tesler
This paper also explains the connections between the space of diagonal harmonics and the Macdonald polynomials with the operator Nabla.

The question that these polynomials have non-negative integer coefficients is still unsettled.

Adapeted from the paper:
A REMARKABLE $q,t$-CATALAN SEQUENCE AND $q$-LAGRANGE INVERSION, Adriano Garsia, Mark Haiman