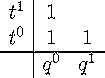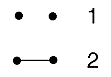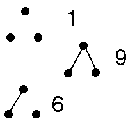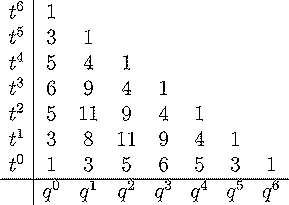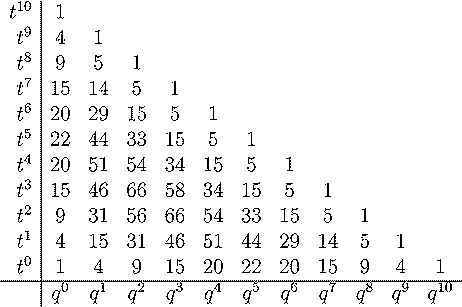The number of rooted forests
The hilbert series for the diagonal harmonics is conjectured to q,t
count the number of rooted forests of trees with labeled verticies.
These numbers arise naturally from an
operator on symmetric functions that has the Macdonald polynomials as eigenfunctions.
Below is a table of these numbers for n between 2 and 6. The total
degree of these polynomials is n(n-1)/2. It
is conjectured that they have non-negative integer coefficients as polynomials
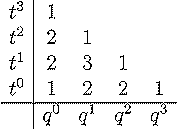
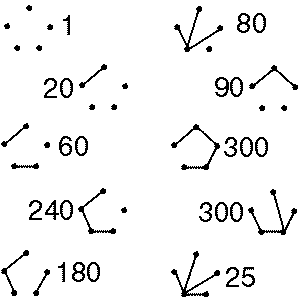
in q and t. Next to the tables 2 through 5 we have placed an image
of forests of trees and next to each forest is the number of ways of labeling
the forest and giving each tree a root (therefore the sum of these numbers
will be (n+1)n-1).
These tables were taken from a much larger set that is available in
postscript/LaTeX form available on the web
page of Mark Haiman. You will also find there the Frobenius series
of the diagonal harmonics up to n=6.
| n=2 |
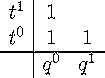 |
 |
| n=3 |
 |
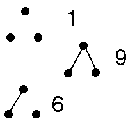 |
| n=4 |
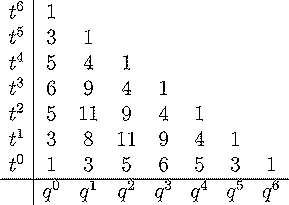 |
 |
| n=5 |
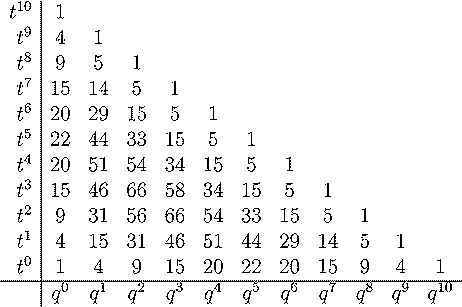 |
|
| n=6 |
 |