HOME:
BACK:	More qt-analogs

The number of standard tableaux of shape lambda

The number of standard tableaux of a given shape is given by the formula

where the product runs over all cells s in partition lambda, a(s) represents the arm of the cell s in lambda, l(s) represents the leg of the cell s in lambda
(a(s) + l(s) + 1 is often refered to as the hook of a cell and so this is called the 'hook length formula').

Related to the Macdonald polynomials one has the q,t-coefficients and referred to as the q,t-Kostka polynomials.

If q and t are both set to 1, we have that and are both equal to the number of standard tableaux of shape lambda.

Conjecture:

The polynomials

(and

) have non-negative integer coefficients and
are a generating function for the number of standard tableaux of shape lambda.

This result (at least the postitivity part) is known for

when it is of the form (2^a1^b), (32^a1^b), (42^a1^b), (a21^b), (a1^b)

when it is of the form (a1^b), (a21^b), (a31^b)
OR the conjugate partition of any of these results.

Note that if q=0 in the polynomial , we have the standard single variable Kostka polynomials which are known to t-count the column strict tableaux of shape and content .

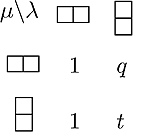
Below are the tables for the transformed q,t-Kostka polynomials for n=2,3 and 4. You may also find these tables up to n=7 in PDF/poscript and LaTeX form on this web site. and Maple programs by Stembridge and Garsia-Tesler.
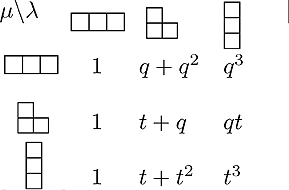
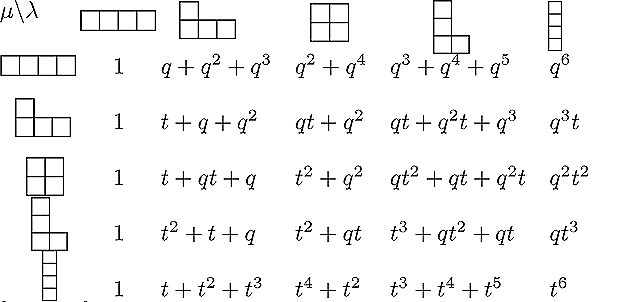
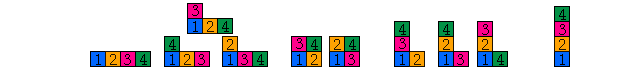