The Rotational Symmetries of the Cube

 

In the first problem of this homework assignment I asked you to find me the size of the symmetry group of all of the platonic solids and the question was quite easy because all you had to do was count the number of ways the cube could be rotated so that the faces were rearranged in some order.  Therefore you are aware that the number of rotations of the cube is 24.  In two of the last four problems on Polya enumeration and Burnside's theorem you need to know something more about the group of rotations of the cube.  If you don't approach this problem in a logical manner then this problem could be hard.

 

So what are those 24 rotations of the cube?

The first is the identity.  Enough said.

 

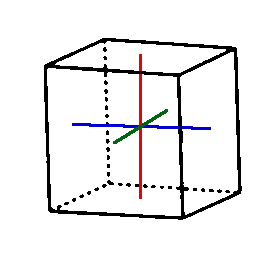
Next consider the 9 rotations of the cube about the 3 axes shown in the picture below.  We can either rotate by 90, 180 or 270 degrees around either the red, blue or green axes.  Each of these rotations will leave two faces fixed and all vertices and edges are not fixed.  When you work out the cycle structure of these 9 elements notice that the 6 rotations by 90 or 270 degrees will have the same cycle structure and the 3 rotations of 180 degrees about each of the axes will have the same cycle structure.

 

Next consider the 6 rotations of the cube by 180 degrees around the 6 axes shown in the image below.  Each of these rotations leave two edges fixed and no faces or vertices fixed.  Each of these 6 permutations will have the same cycle structure.

 

 

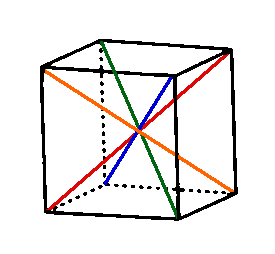
Finally we have rotations by 120 and 240 degrees around the 4 axes shown in the image below.  This gives 8 permutations each of which leave 2 vertices fixed and no edges or faces fixed.  All 8 of these permutations will have the same cycle structure.

 

 

Since we have 1+9+6+8 = 24 permutations we need not look any further for others. We must have the whole group because we found in the very first problem in this homework assignment that there were only 24.