Schedule

Date and Time	Speaker	Title (click titles for abstract)
25 January, 1pm-2pm	Kiumars Kaveh	Multiplicities of ideals and volume of convex diagrams The notion of (Samuel) multiplicity of an ideal I in a local ring R generalizes the fundamental notion of intersection multiplicity of subvarieties in a variety. Focus of much research in commutative algebra has been on its definitions/extensions, properties and computation. In this talk we make a connection between the notion of multiplicity and convex geometry. More precisely to each (primary) ideal in a (large class of) local rings of dim n, we associate a convex set (diagram) in the positive orthant R_+^n such that the volume of the complement of the diagram gives the multiplicity of the ideal. This can be considered as the local version of the theory of Okounkov bodies (of linear systems) and extends the notion of Newton diagram of a monomial ideal (in a polynomial algebra). For the most part the talk is accessible to anyone with just basic knowledge in algebra and geometry. This is joint work with Askold Khovanskii.
25 January, 2:30pm-3:15pm	Yong-Su Shin	Some applications of star-configurations in $P^n$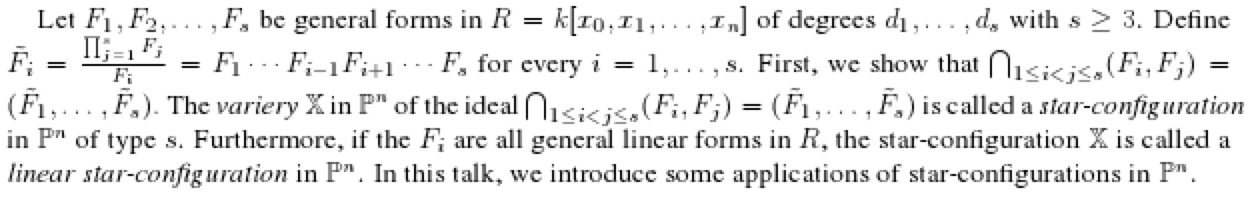
25 January, 3:30pm-4:15pm	Uwe Nagel	Enumerations deciding the Weak Lefschetz Property For proving one implication of the g-theorem on simplicial polytopes, Stanley established the Weak Lefschetz Property of their Stanley-Reisner ring. Deciding the presence of this property is often a difficult problem. We propose an approach for studying monomial ideals in three variables via lozenge tilings of certain planar regions. It provides combinatorial interpretations for the weak Lefschetz property. As a consequence, the presence of the weak Lefschetz property can be decided in new cases. Attention is also given to ground fields of positive characteristic
26 January, 9:30am-10:30am	Frank Sottile	Galois groups of Schubert problems Building on work of Jordan from 1870, in 1979 Harris showed that a geometric monodromy group associated to a problem in enumerative geometry is equal to the Galois group of an associated field extension. Vakil gave a geometric-combinatorial criterion that implies a Galois group contains the alternating group. With Brooks and Martin del Campo, we used Vakil's criterion to show that all Schubert problems involving lines have at least alternating Galois group. My talk will describe this background and sketch a current project to systematically determine Galois groups of all Schubert problems of moderate size on all small classical flag manifolds, investigating at least several million problems. This will use supercomputers employing several overlapping methods, including combinatorial criteria, symbolic computation, and numerical homotopy continuation, and require the development of new algorithms and software.
26 January, 11:00am-11:45am	Hugh Thomas	Higher-dimensional analogues of tropical cluster structures Various tropical aspects of cluster structures (exchange relations, g-vectors) generalize naturally beyond the setting of cluster algebras. I will explain this, based on arXiv:1001.5437 joint with Steffen Oppermann, and also subsequent joint work with Steffen Oppermann and Charles Paquette. This talk could also serve as an introduction to the tropical aspects of cluster algebras.
26 January, 1:30pm-2:15pm	Liz Beazley	Projections on Parabolic Quotients of Affine Weyl Groups Affine Weyl groups and their parabolic quotients are used extensively as indexing sets for objects in representation theory, algebraic geometry, and number theory. Moreover, we can conveniently realize the elements of certain quotients via intuitive geometric and combinatorial models such as abaci, alcoves, root lattice points, and core partitions. Berg, Jones, and Vazirani have described a bijection between n-cores with first part equal to k and (n-1)-cores with first part less than or equal to k. This bijection also has an interpretation in terms of the correspondence of Lapointe and Morse between n-cores and (n-1)-bounded partitions. This correspondence played a crucial role in the development of k-Schur functions, which are known to represent the Schubert basis in the homology of the affine Grassmannian. In this talk we discuss how to generalize this bijection of Berg, Jones, and Vazirani to parabolic quotients of affine Weyl groups in other classical Lie types. We have developed not only combinatorial techniques to describe this map, but also a visually explicit method utilizing the geometric properties of the alcove model coming from the root system associated to the affine Weyl group.
26 January, 3:00pm-4pm	Sara Faridi	Monomial Resolutions This talk is about combinatorial techniques to investigate minimal resolutions of monomial ideals. We focus in particular on the projective dimension (the length of a minimal free resolution) and how to bound or compute it using the combinatorics of the monomial ideal.
27 January, 9am-9:45am	Ilias Kotsireas	Hadamard and skew-Hadamard matrices of new orders Hadamard and skew-Hadamard matrices are supposed to exist for every order n such that n is a multiple of 4. Even though there are several infinite classes and constructions for Hadamard and skew-Hadamard matrices, these well-known conjectures are open for more than 100 years. We report on recent computational progress on these conjectures, namely the discovery of Hadamard and skew-Hadamard matrices of new orders. This progress is mainly due to a recent algorithmic breakthrough. This is joint work with D. Djokovic (U. Waterloo) and O. Golubitsky (Google Inc). PLEASE NOTE: Ilias sends his regrets and will be unable to come, so this talk has been cancelled
27 January, 10:00am-10:45am	Leila Khatami	The poset of the nilpotent commutator of a nilpotent matrix
27 January, 11:30am-12:30pm	Thomas Lam	Positroid varieties The positroid stratification of the Grassmannian $G(k,n)$ is the intersection of the cyclic rotations of the Schubert stratification. This stratification was studied extensively in Postnikov's work on total positivity of the Grassmannian. It also appears in the study of Poisson geometry, Frobenius splitting, KP solitons, scattering amplitudes,... I will discuss some combinatorial, cohomological, and geometric properties of this stratification. This talk will be based on joint work with Allen Knutson and David Speyer.