Schedule
Dates are listed in reverse-chronological order. Unless otherwise indicated, all talks will take place on Monday from 15:00-16:00 in N638 Ross Building (York University).
Date Speaker Title (click titles for abstract) 13 Apr. 2015*
2-3pmGreg Warrington
(U. of Vermont)The sweep map and the rational Catalan numbers The zeta map has been rediscovered by many researchers in various contexts. Our interest ultimately stems from its ability to relate the area, bounce and dinv statistics that arise in the study of the q,t-Catalan numbers. I'll discuss some aspects of both the general sweep map, which applies to words over arbitrary alphabets and arbitrary weights, as well the relationship of the rational zeta map to the rational q-Catalan. Some of what I discuss is joint work with N. Loehr and D. Armstrong.13 Apr. 2015*
3-4pmJim Haglund
(U. of Pennsylvania)Some new interpretations for the (q,t)-Schroder and (q,t)-Narayana numbers We discuss a recent extension, due to Remmel, Wilson, and the speaker, of the well-known "shuffle conjecture" for the character of the space of diagonal harmonics. We then show how this extension leads to some new expressions for the (q,t)-Schroder and (q,t)-Narayana numbers.30 Mar. 2015 Hugh Thomas
(U. of New Brunswick)A Fuss-Catalan generalization of c-sortable elements Let W be a finite Weyl group. Two of the important classes of Catalan objects associated to W are the clusters and the noncrossing partitions. These both have well-understood Fuss-Catalan generalizations. A third important class of Catalan objects are the c-sortable elements of W, originally introduced by Reading in order to connect clusters and non-crossing partitions. I will describe a Fuss-Catalan generalization of c-sortable elements, and say something about how they relate to other Fuss-Catalan objects. This talk will be based on joint work with Christian Stump and Nathan Williams, arXiv:1503.00710.23 Mar. 2015 Karola Meszaros
(Cornell U.)Subword complexes via triangulations of root polytopes Subword complexes are simplicial complexes introduced by Knutson and Miller to illustrate the combinatorics of Schubert polynomials and determinantal ideals. They proved that any subword complex is homeomorphic to a ball or a sphere and asked about their geometric realizations. We show that a family of subword complexes can be realized geometrically via triangulations of root polytopes. This implies that a family of $\beta$-Grothendieck polynomials are special cases of reduced forms in the subdivision algebra of root polytopes. Based on joint work with Laura Escobar.16 Mar. 2015 Iva Halacheva
(U. of Toronto)A cactus group action on crystals and the shift of argument algebras For any crystal of a representation V of a finite-dimensional semisimple Lie algebra g, we define an action of the corresponding cactus group Jg and hence also of the quotient pure cactus group PJg via Schutzenberger involutions. On the other hand, PJg is the fundamental group of a space Mg which parametrizes a family of maximal commutative subalgebras of U(g) - the shift or argument algebras. These subalgebras have simple spectrum when acting on V, and so give a covering of Mg. When g is of type A, the resulting monodromy action of PJg coincides with the action on crystals. We conjecture that this is also true in general. Further in type A, using skew-howe duality for crystals we can relate this to Henriques and Kamnitzer's cactus group action on tensor products of crystals and another family of maximal commutative subalgebras in the n-th tensor product of U(g) - the Gaudin subalgebras. This is joint work with Joel Kamnitzer, Leonid Rybnikov and Alex Weekes.9 Mar. 2015 Matthias Beck
(San Francisco State U.)Permutation Descent Statistics via Polyhedral Geometry Permutations are some of the most fundamental objects of mathematics, and a basic combinatorial statistics of a permutation π ∈ Sn is the number of descents, des(π) := #{ j : π(j) > π(j+1) }. Euler realized that
∑k ≥ 0 (k+1)n tk = ( ∑π ∈ Sn tdes(π) ) / (1-t)n+1
and there have been various generalizations of this identity, most notably when Sn gets replaced by another Coxeter group.We will illustrate how one can view Euler's identity (and its generalizations) geometrically through enumerating integer points in certain polyhedra. This gives rise to "short" proofs of known theorems, as well as new identities.
This is joint work with Ben Braun (Kentucky).
2 Mar. 2015 Canceled 23 Feb. 2015
NO SEMINAR16 Feb. 2015
NO SEMINARFamily Day (Univeristy is closed) 9 Feb. 2015 Ryan Kaliszewski
(Drexel U.)Combinatorial fillings and their correspondence with reverse plane partitions Ryan Kaliszewski and Jennifer Morse (Drexel University)
Inspired by the long-standing open problem to combinatorially characterize the Macdonald symmetric functions, Austin Roberts recently introduced a new combinatorial structure and proved that the Lascoux-Schützenberger charge/tableaux formulation for the q=0 Macdonald polynomials can instead be written using these combinatorial objects with the major index statistic. We have discovered that a variation on these objects newly characterize Schur and Grothendieck polynomials (representatives for cohomology and K-theory classes, respectively), and lends itself to an alternate view on classical combinatorial formulas such as the Littlewood-Richardson rule and the hook-length formula for standard Young tableaux.2 Feb. 2015 Mike Zabrocki
(York U.)Macdonald symmetric functions and parking functions A parking function can be thought of as a Dyck path of length n where the vertical edges are labeled with the integers 1 through n, increasing in the columns. For example,
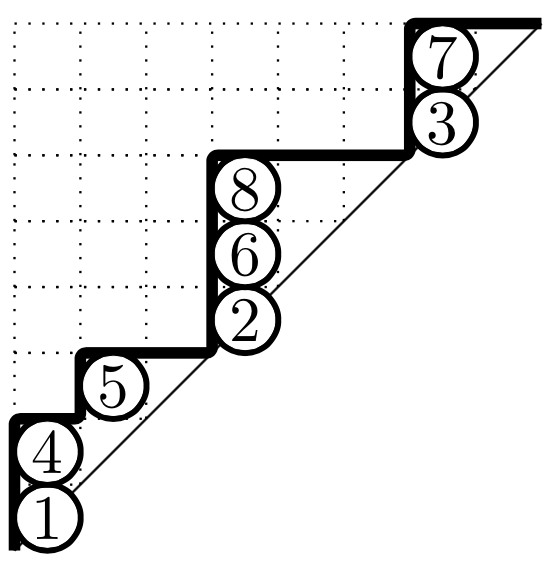
is a parking function of 8 and it touches the diagonal according to the composition (3,3,2).
Haglund's "shuffle conjecture" from 2005 is a combinatorial formula for the symmetric function expression for nabla(e_n) with one term for each parking function. In 2008 Haglund, Morse and myself extended this conjecture to the action of nabla on a symmetric function indexed by a composition. The combinatorial formula has one term for each parking function which touches the diagonal according to the composition.
In the last few years Hicks, Garsia, Xin and myself were partially able to prove the compositional shuffle conjecture by showing algebraic recurrences on coefficients exist and agree with the combinatorics. In this talk I'll show algebraic recurrences which generalize those that were used to prove those results and draws a direct connection with Macdonald symmetric functions.26 Jan. 2015 Amy Pang
(LaCIM, UQAM)Card-shuffling and Convolutions of Projections on Graded Hopf Algebras Diaconis, Pitman and Fill studied many models of card-shuffling where a deck is cut into piles according to some distribution, then interleaved randomly. We observe that the transition probabilities of these shuffles can be expressed in terms of certain "convolutions of projections" operators on the shuffle algebra. I will explain how to mimic this connection to model the breaking-then-recombining of other combinatorial objects, such as partitions. The structure of the underlying Hopf algebras gives a lot of information about these processes.19 Jan. 2015 Emily Redelmeier Cartography on unoriented surfaces and combinatorial techniques for real and quaternionic random matrices I will be discussing applications of combinatorial topology to random matrix theory. In particular, I will discuss an encoding of graphs in surfaces in the symmetric group, and its generalization to the nonorientable surfaces which appear when we are considering real or quaternionic random matrices. I will then show how these tools may be connected to free probability. I will discuss second-order freeness: free probability applied to the fluctuations of random matrices, and how the behaviour of matrices differs between the complex, real, and quaternionic cases.1 Dec. 2014 Diana Ojeda
(U. of Toronto)Finite forms of Gowers' Theorem on the oscillation stability of c_0 I will present an example of the interaction between Ramsey Theory and Geometry of Banach Spaces. Hindman's Theorem states that given any 2-coloring of FIN, the collection of finite sets of natural numbers, there exists an infinite sequence of elements of FIN all of whose finite unions get the same color. Gowers formulated and proved a generalization of Hindman's Theorem to obtain the oscillation stability of c_0, the space of real sequences converging to 0 endowed with the supremum norm. Namely, he proved that any Lipschitz function defined on the unit sphere of c_0 is almost constant on the unit sphere of some infinite dimensional subspace.
In this talk I will first translate the oscillation stability of c_0 into the language of Ramsey Theory. Then, I will present a combinatorial proof of a finite version of the resulting Ramsey type theorem. It is worth pointing out that Gowers' argument uses ultrafilter dynamics, and up to now there is no combinatorial proof of the original (infinite) version of this theorem.24 Nov. 2014 Rafael S. Gonzalez
(U. of Kentucky)On the free Lie algebra with multiple brackets We explore a beautiful interaction between algebra and combinatorics in the heart of the free Lie algebra on n generators: The multilinear component of the free Lie algebra Lie(n) is isomorphic as a representation of the symmetric group to the top cohomology of the poset of partitions of an n-set tensored with the sign representation. Hence, we can understand the algebraic object Lie(n) by applying poset theoretic techniques to the poset of partitions whose description is purely combinatorial. We will show how this relation generalizes further in order to study free Lie algebras with multiple compatible brackets. In particular we obtain combinatorial bases and compute the dimensions of these modules answering a question posed by F. Liu.17 Nov. 2014 Yannic Vargas
(LaCIM, UQAM)NCQsym revisited: a packed words approach The hopf algebra NCQSym (aka WQSym) is a natural generalization of the Hopf algebra of permutations FQSym, introduced by N. Bergeron & M. Zabrocki (2006) / F. Hivert (1999) / F. Chapoton (1999)/ A. Jöllenbeck (1997)(independently, from different points of view). A basis of NCQSym is given by sets compositions, who are also equivalent to packed words. When studying this hopf algebra from the packed words point of view, it is not difficult to generalize some properties from FQSym to NCQSym. We discuss this approach, introduce analogous of the monomial basis to NCQSym and give an application to the study of the Drinfeld double of FQSym and NCQSym.10 Nov. 2014
NO SEMINAR(due to travel) 3 Nov. 2014 Vincent Genest
(U. de Montréal)The Bannai-Ito algebra, its q-extension and some applications In this talk, I will present the Bannai-Ito algebra together with some applications. Its relation with the Bannai-Ito polynomials, the Racah problem for the paraboson algebra and a quantum superintegrable system with reflections will be surveyed. Its q-extension, and the relation it has with osp_q(1|2), will also be discussed.27 Oct. 2014 Kevin Dilks
(U. of Minnesota)q-gamma nonnegativity A polynomial of degree n with symmetric coefficient sequence has a unique expansion in terms of the polynomials t^i(1+t)^(n-2i). Gal has conjectured that for the h polynomial of generalized homology spheres (which includes simplicial polytopes), this expansion has nonnegative coefficients. In this talk, we will describe a multivariate formulation of this property, and give examples of proven and conjectured results for well-known combinatorial objects like the associahedron and the Coxeter complex.20 Oct. 2014 Salvatore Stella
(North Carolina State U.)d-vector fans for cluster algebras of finite and affine type Thanks to the Laurent phenomenon a family of integer vectors (the d-vectors) can be naturally associated to each cluster algebra. This family encodes many of the combinatorial properties of the algebra itself making it an interesting object to study. In this talk, after reviewing the basic definitions, we will construct the d-vectors associated to any finite or affine type cluster algebra with an acyclic initial seed. The construction will leverage some interesting features of the action of a particular product of reflections on the associated root system.13 Oct. 2014
NO SEMINARThanksgiving 6 Oct. 2014 Suho Oh
(Texas State U.)Wires and separation Wiring diagrams are widely used combinatorial objects that are mainly used to describe reduced words of a permutation. In this talk, I will mention an interesting property about those diagrams, and then introduce other results and problems related to this property.3 Oct. 2014* Christophe Hohlweg
(LaCIM, UQAM)Weak order and imaginary cone in infinite Coxeter groups The weak order is a nice combinatorial tool intimately related to the study of reduced words in Coxeter groups. In this talk, we will discuss a conjecture of Matthew Dyer that proposes a generalization of the framework weak order/reduced words to infinite Coxeter groups. On the way, we will talk of the relationships between limits of roots and tilings of their convex hull, imaginary cones, biclosed sets and inversion sets of reduced infinite words (partially based on joint works with M. Dyer, J.P. Labbé and V. Ripoll).29 Sep. 2014 Brendan Pawlowski
(U. of Minnesota)Permutation patterns and Stanley symmetric functions Given a permutation w, Stanley defined a symmetric function F_w which encodes information about the reduced words of w, and showed that F_w is a single Schur function exactly when w avoids the pattern 2143. We generalize this statement, showing that the Schur expansion of F_w respects pattern containment in a certain sense, and that the number of Schur function terms is determined by pattern avoidance conditions on w. Along the way, we compute the cohomology of certain subvarieties of Grassmannians, resolving some cases of a conjecture of Liu. Our proofs use the diagram Specht modules introduced by James and Peel, which in this case are closely related to the Schubert modules of Kra?kiewicz and Pragacz. This is joint work with Sara Billey.15 Sep. 2014 Joshua Hallam
(Michigan State U.)Factorization of the Characteristic Polynomial of a Poset The characteristic polynomial of a poset is the generating function for the Mšbius function of the poset. For some families of posets, the polynomial factors with nonnegative integer roots. We will present a new method which gives a combinatorial explanation for these factorizations. Additionally, we will see how this method can be used to explain a relationship between the generating function for the increasing forests of a graph and its chromatic polynomial. This is joint work with Bruce Sagan.8 Sep. 2013
Bruce Sagan
(Michigan State U.)Of antipodes and involutions, of cabbages and kings ... If H is a connected, graded Hopf algebra, then Takeuchi's formula can be used to compute its antipode. However, there is usually massive cancellation in the result. We show how sign-reversing involutions can sometimes be used to obtain cancellation-free formulas. We apply this idea to the Hopf algebras of polynomials, graphs, and noncommutative symmetric functions. This is joint work with Carolina Benedetti.