Do your own work. Don't look for a solution on the web or take one from another
student's work unless you already have found your own solution and intend to
review another to make a comparison. Work that is not original will be graded
accordingly. Presenting someone else's work as your own without proper citation
is academic dishonesty. You must cite any internet sources which you have consulted.
You will be required to take the
York University Academic Integrity Tutorial.
Participation: You are expected to show your commitment to this course
and your fellow students by sharing your mathematical knowledge and your feelings
about the material. Attendance at the weekly classes and the tutorials is
obligatory and you will lose 2 points from your course grade for each class
or tutorial that you miss each term. Sometimes attendance at the weekly classes
will be measured by a short in class assignment. Non participation in these assignments
will result in a lowering of your participation grade. Note that participation is
not a percentage of your grade, but non-participation and attendance can lower
your overall score.
Assignments: There will be roughly one assignment 4-5 weeks. Most
assignments will require explanation beyond a simple one or two word/numerical answer.
It is good practice to RECOPY THE QUESTION EVERY SINGLE TIME when you do the
assignment. This makes it possible to understand what the assignment when it is
handed back to you and it attempts to reduce the error of answering a different
question than is on the assignment. Full credit is given to papers which demonstrate
deep understanding of the problem by providing multiple solutions and considers
variations based on the original question when this is appropriate.
Your assignment should include complete
sentences and explanations and not just a few equations
or numbers. A solution will not receive full credit unless you explain
what your answer represents and where it came from.
You may discuss the homework
with other students in the class, but please write
your own solutions.
Note: Late assignments will be penalized by 20% per day. This will apply to
any homework handed in after the class time in which it is due. In addition,
assignments which are handed in late are unlikely to be marked in a timely manner.
Tutorial Assignments: You are expected to continue working on the
problems discussed in class and in the tutorials and to keep a running record of
the problems from those exercises (these will be listed on the web page) as well as your progress and
the development of a solution for them.
Here is a breakdown of some aspects that I plan to evaluate your solutions from the tutorial:
(1) The discussion begins with an explanation of the problem
(2) The explanation should convince the reader that the meaning of the question is understood
(e.g. small examples, a clearly labeled table of data, and/or a discussion of the meaning of the question)
(3) diagrams, tables or images that are drawn to aid the reader in understanding the problem
are well labeled and explained
(4) Clear statements are made of conjectures that are believed to be true
(5) Explanations of why those conjectures are true are included
(6) An explanation of how the problem solving process proceeded is clear from the explanation
(7) The entries consist of writing which is clear and grammatically correct
(8) A conclusion about the solution to the problem is reached
On both your journals and assignments, I will be looking for evidence of your solutions demonstrating
one of the following 4 levels of understanding:
Level 4: Deep understanding of the problem. Complete solution carefully presented.
Provides multiple alternative solutions where possible. Considers variations based
on the original question (with or without solutions).
Level 3: Good understanding of the problem. Problem solved or a solution provided which can easily
be completed, for example, one with a minor error which would be simple to correct. No evidence
of engagement beyond finding an answer to the problem as posed.
Level 2: Incomplete understanding of the problem. Limited progress to solution or a solution marred by major errors.
Level 1: Minimal understanding of the problem. Work submitted shows little progress toward solution.
Note that to receive full credit you must go beyond simply solving the problem as posed. Learn to think of
your solutions as a starting point.
Quizzes and Final Examination: There will be 3 quizzes per term (dates listed below).
A final examination will be
scheduled for the April exam period and the date announced in late-February/early March.
(Sept 1, 2011) The textbook for this course "Thinking Mathematically" currently has a new edition.
If you have a older edition of this textbook it should suffice.
(Sept 1, 2011) Those that would like to review some concepts that you are
expected to have from high school, there are a few online references
I can recommend to start:
(1) There is a quite extensive set of algebra tutorials, covering
a wide range of topics, maintained by West Texas A&M University.
The URL for the main page of this resource is
http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra
though a quicker way to get to this page is via the link on the Bethune
College Math Help page,
http://www.yorku.ca/bethune/math
(2) There is also a detailed online course in Trig basics, which starts
right from the beginning, the URL for the main page of the course being
http://www.yorku.ca/bethune/math/trig.html
(as you can guess from this URL, the Bethune Math Help page has
a link which takes you to the Trig course main page).
Other potentially useful information is also listed on the Bethune
Math Help web page, and further online resources will be added there
as they become available.
(September 19, 2011) I wasn't able to meet the class on Monday September 12 but class was held by Dorota Mazur that evening. She gave you
an in class assignment that I labelled 'assessment quiz.' I wanted to make sure that you had some basic algebra skills that you will be using
in almost all of your math courses: exponents, logarithms, trig functions, manipulations of polynomials, functions and pattern recognition. There
were 11 questions in total (5 questions but 2 of them had 4 parts each). In total 31 people took the quiz.
| number of problems correct |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| number of papers |
2 |
1 |
1 |
6 |
1 |
3 |
7 |
3 |
5 |
2 |
The reason why I gave this assessment quiz is that I would like you to know some of the things you should be reviewing in order to do
well in this class and your other math courses. The question people had the hardest time with was the last one with logarithms.
Hint: it is a good idea to review properties of logarithms and the definition.
(September 26, 2011) The link listed above to
the few pages of text from Krantz's book
is useful for understanding telescoping sums. Make sure you try the following three examples:
\[
1^2 +2^2 + \cdots + n^2 = n(n+1)(2n+1)/6
\]
\[
1\cdot 2+ 2\cdot 3 + 3 \cdot 4 + \cdots + n(n+1) = n(n+1)(n+2)/3
\]
\[
1\cdot 2\cdot 3\cdot 4 +2\cdot 3\cdot 4\cdot 5 +3\cdot 4\cdot 5\cdot 6 +\cdots + n(n+1)(n+2)(n+3) = n(n+1)(n+2)(n+3)(n+4)/5
\]
Challenge:
What is the general formula? Write it down and show why it is true.
(October 2, 2011) Note you should hand your solutions to your tutorial
problems AT THE BEGINNING of your tutorial (usually 2 weeks later).
(October 3, 2011) If you are interested in finishing the logic problem it is here:
First past the post. It isn't too hard if you make the right observation.
We finished it before we cleared the
classroom.
(October 4, 2011) I wrote a few notes on telescoping sums for those of you that have
a hard time with them.
(October 17, 2011) The topic of logic that we are discussing in class can be found in
Chapter 2 of the book MP:ATAM.
(October 24, 2011) I suggested last week that for practice that you try 2.17, 2.32 and 2.39.
Actually, you should do lots of problems. It is the best way of learning mathematics.
(November 21, 2011) This week I took some time to talk about how to succeed in this course (and
all your courses for that matter). If you enjoyed the audio that I played, it comes
from
This American Life. Here is my advice:
(1) Start your homework early.
(2) Practice for the quizzes.
(3) Do problems. Lots of them. If you don't understand the problems, only then read the book for clarification and ideas.
(4) Stuck? Remember to apply all your methods from Lecture #3 Sept 26, 2011. Never give up.
(5) Never get a 0 on an assignment for not handing it in.
(6) Go to math lab (find out when the TAs for the class are there).
(7) Work on your homework and study for quizzes in groups.
(8) Go to my office hours M5-6 and Th4:30-5:30.
(9) email me or the TAs (this is not ideal because it is often hard to communicate what needs
clarification by email, but if you need a hint, help or to make an appointment to see me,
this could work).
(November 28, 2011) I posted the next homework assignment that isn't due until January. My advice: start now.
For those of you in Tutorial 1, please take a look at the
number spirals
instructions. There were a bunch of errors and clarifications that didn't get done until after the
tutorial on November 21 and that have now been corrected on the pdf that is here.
(December 5, 2011) Starting January 16 there will be 5 tutorials left and we are going to ask
you (the students) to get in groups of 2-3 and present the problems. This will
require some preparation and the tutorial problems will be made available in advance.
(December 5, 2011) There was a typo on problem 1 (a) of the homework. Please download
the new copy and change the word 'even' to 'odd' in two places in the problem. The
problem was clearly false before.
(January 3, 2012) Welcome back. Here is an announcement that I received by email today
that is relevant for our class. I never remember to make these announcements in class.
Hello All,
Please make an announcement in your classes regarding the upcoming Mathematical Contest in
Modeling (MCM).
The MCM is a contest where teams of undergraduates use mathematical modeling to
present their solutions to real world problems. Each team can have a maximum of
three members who work together to find a solution to one of three posed problems.
The solution may include mathematics as well as computer simulation. The team must
also write a report on their solution. Problems are designed to be open-ended and
are unlikely to have a unique solution. Attention must be focused on clarity,
analysis, and design of the solution.
The MCM will take place on February 9-13, 2012. If students have any questions
regarding the MCM they may email me (jmheffer@mathstat.yorku.ca) or look at the
MCM website http://www.comap.com/undergraduate/contests/. If they are interested
in participating they should email me by Jan 15. There will be an information/training
session in late January.
Cheers,
Jane
(January 23, 2012) The class has already been broken into groups for presenting tutorial
problems. I'll place your names in the tutorial meeting schedule below for your presentations. You will get the tutorial problem
at least one week in advance. I have placed some
instructions about how to prepare for your presentation. I would like
you to give me a writeup the week after (or the same day if you like) of your answers to the questions.
(February 6, 2012) When we did induction in small groups on January 23 I gave you the following problems. You should figure out for what values of $n$ the statements
are true and then prove them by induction:
A. \[1^3+2^3+3^3+\cdots+n^3 = \frac{n^2(n+1)^2}{4}\]
B. \[1^2+3^2+5^2+\cdots+(2n-1)^2=\frac{n(4n^2-1)}{3}\]
C. \[1^2+4^2+7^2+\cdots+(3n-2)^2=\frac{n(6n^2-3n-1)}{2}\]
D. \[1 + 2 + 4 + 5 + 7 + \cdots + (3n-1) + (3n+1) = 3n^2+3n+1\]
E.
\[ \frac{a^{n}- b^n}{a-b} = a^{n-1} + a^{n-2} b + a^{n-3} b^2 + \cdots + b^{n-1} \]
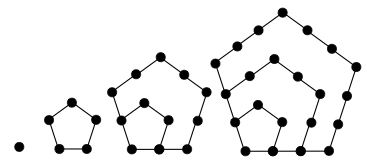
F. If $a_n = $ the number of dots in the $n^{th}$ diagram below (where the next diagram is equal to the previous one plus three extra segments each containing $n$ dots), then
$a_n = \frac{3n^2 - n}{2}$.
G. \[ \begin{bmatrix} 1 & 1\\0&1\\\end{bmatrix}^n = \begin{bmatrix} 1 & n\\0&1\\\end{bmatrix} \]
(February 6, 2012) I am modifying the homework assignment and adding new rules. If you got 9, 10, 11 or 12 on the fourth quiz, I don't care if you hand in
this assignment and I give you a free pass on it. If you got a 6,7,8 on the quiz I would like you
to do the homework as planned. If you got less than 6 on the quiz, then you must do ALL THE
PROBLEMS ON THIS PAGE. I am considering making this the rule for future homework assignments where the number of problems you have to do
to get full credit is inversely proportional the the score that you get on the quiz.
(February 6, 2012) I gave you a problem for next time. Say that the sequence $F_0 = 0, F_1 = 1, F_2 = 1$, and $F_{n+1} = F_n + F_{n-1}$ for $n\geq 2$. Show by induction that
\[ \begin{bmatrix} 1 & 1\\1&0\\\end{bmatrix}^n =
\begin{bmatrix} F_{n+1} & F_{n}\\F_{n}&F_{n-1}\\\end{bmatrix} \]
(February 14, 2012) One more example of an induction problem (in case you were sick of them already). Let the sequence $a_n$ be defined recursively as follows: $a_0 = a_1 = 1$ and $a_n = 3 a_{n-1} - 2 a_{n-2} + 2$ for
$n\geq 2$. Show that $a_n = 2^{n+1} - (2n+1)$ for $n\geq 0$. This one was an important example because you can't use just the normal inductive assumption and base case. This is 'strong induction' in your book.
(February 14, 2012) For homework, I would like you to look up (and learn) the definition of one-to-one. It is in your book, but you should be able to find it on wikipedia or other online sources as well. There are only a few things that I will ask that you memorize in this class: one of them is the definition of 'divides', another is the definitions we just covered: 'function,' 'onto' and 'one-to-one.'
(March 20, 2012) I've posted homework 6 for practice. Don't worry about handing it in, but be sure to do the questions.
(March 23, 2012) I love
XKCD.

(March 31, 2012) I've updated my office hours April 2, 5-6pm; April 5, 2-3pm; April 9 at 3-4:30pm.
(April 5, 2012) The tutorial problem is due April 9 for tutorial 2. You may either bring it
to my office hours or you may bring it to the final exam on the 11th and hand it in then.
Make sure that if you have any outstanding work that you have not handed in that you
also bring that to the final exam. One thing that I did not receive from a number of
people is an explanation of the presentation that you did in the tutorial (you should hand
in one per group).
Lecture meeting schedule
Date
|
Topic
|
Notes
|
Sept 12
|
Intro to course, sample problem, assessment quiz
|
|
Sept 19
|
the difference between conjecture and proof, the technique of telescoping sums
|
hw #1 assigned
|
Sept 26
|
how to make a conjecture and then explain it, telescoping sum example
|
|
Oct 3
|
logic and logic puzzle
|
Quiz 1
|
Oct 10
|
reading week, no class
|
|
Oct 17
|
truth tables, tautologies, contradictions and fallacies
|
hw #1 due
|
Oct 24
|
quantified logical statements
|
hw #2 assigned
|
Oct 31
|
Proving statements true or false, vacuous and trivial
|
return hw 1
|
Nov 7
|
definition of divides, direct proof
|
Quiz 2
|
Nov 14
|
go over quiz 2, definition of transitive order
|
return quiz 2, hw #2 due
|
Nov 21
|
pep talk (see remark above), examples of proofs
|
return hw 2
|
Nov 28
|
Examples of proof in groups presented on the board
|
HW #3 given
|
Dec 5
|
Mostly just did the quiz
|
Quiz 3
|
Jan 9
|
Went over the quiz, homework was "prove $\sqrt{11}+\sqrt{13}$ is irrational"
|
return quiz 3
|
Jan 16
|
irrational proof, Polya strikes out
|
HW #3 due
|
Jan 23
|
induction
|
HW #4 assigned
|
Jan 30
|
|
Quiz 4
|
Feb 6
|
Go over the quiz and homework
|
return quiz #4 and homework #3
|
Feb 13
|
A bit more induction, definition of a function and onto, played: 'is it onto?'
|
|
Feb 20
|
reading week, no class
|
|
Feb 27
|
1-1 and onto
|
HW #4 due, HW#5 assigned
|
Mar 5
|
|
Quiz 5
|
Mar 12
|
relations, transitive, reflexive, symmetric
|
return quiz #5
|
Mar 19
|
relations again, binomial coefficients, Pascal's triangle and paths in a rectangle
|
HW #5 due, hw #6 assigned
|
Mar 26
|
more binomial coefficients and paths
|
|
Apr 2
|
|
Quiz 6
|
Tutorial meeting schedule - NOTE: Tutorial 1 is held in Ross S156 and Tutorial 2 is held in Ross S101
Date
|
Topic
|
Notes
|
Sept 12
|
won't meet because tutorials don't meet first week of Fall
|
|
Sept 19
|
Diagonals of a Rectangle
|
Tut 1
|
Sept 26
|
Diagonals of a Rectangle
|
Tut 2
|
Oct 3
|
first tutorial problem due, cells of a prism
|
Tut 1
|
Oct 10
|
reading week, no class
|
|
Oct 17
|
first tutorial problem due, cells of a prism
|
Tut 2
|
Oct 24
|
second tutorial problem due, Square Bashing
|
Tut 1
|
Oct 31
|
second tutorial problem due, Square Bashing
|
Tut 2
|
Nov 7
|
third tutorial problem due, non-transitive dice
|
Tut 1
|
Nov 14
|
third tutorial problem due, non-transitive dice
|
Tut 2
|
Nov 21
|
fourth tutorial problem due, number spiral
|
Tut 1
|
Nov 28
|
fourth tutorial problem due, number spiral
|
Tut 2
|
Dec 5
|
fifth tutorial problem due, Archimedes' Regions
|
Tut 1
|
Jan 9
|
fifth tutorial problem due, Archimedes' Regions
|
Tut 2
|
Jan 16
|
6th due, (Andy Koh, Ajki Lolja, Yan Xu) counting rectangles
|
Tut 1
|
Jan 23
|
6th due, (Injy Raad, Michael Rutledge, Dhruv Popli) counting rectangles
|
Tut 2,3
|
Jan 30
|
7th due, (Peter Le, JiaHao Yu) escalators
|
Tut 1
|
Feb 6
|
7th due, (Raluca Antonescu, Jasdeep Dhaliwal) escalators
|
Tut 2,3
|
Feb 13
|
8th due, (Blessing Enitan, Talmai Lamont) number grids
|
Tut 1
|
Feb 20
|
reading week, no class
|
|
Feb 27
|
8th due, (Ali Hajmanouchehri, Chao Zhang, Nu Chen) number grids
|
Tut 2
|
Mar 5
|
9th due (Joelle Chung, Joshviraj Gunesh, Rima Belousova) dividing an inheritance
|
Tut 1
|
Mar 12
|
9th due, (Christopher Couto, Henok Weldyes, Stephen Lidderdale) dividing an inheritance
|
Tut 2
|
Mar 19
|
10th due, (Jian Wang, Syad Asghar, Yixin Yang) around the table
|
Tut 1
|
Mar 26
|
10th due, (Emmaz Rastgar, Giasuddin Ahmed Kazi, Zohaib Ratani) around the table
|
Tut 2
|
Apr 2
|
Review
|
MEET IN Ross S156
|