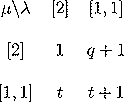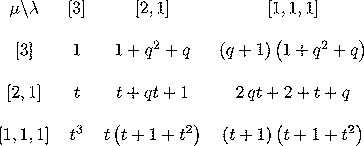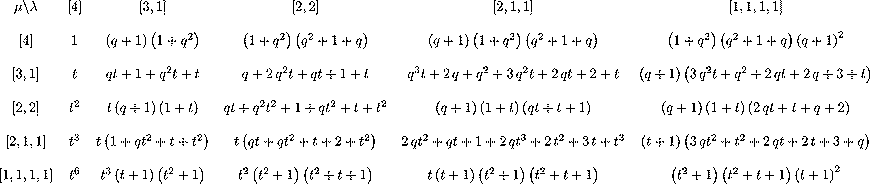q,t-Binomial coefficients
The q,t-binomial coefficients are the coefficients of m_\lambda
in the symmetric function Hµ(X;q,t)
(or the wiggled version). Below we show some tables of these
polynomials. The conjecture that they are polynomials with non-negative
integer coefficients follows from the same result for the q,t-Kostka
polynomials. There is an interesting pair of relations between
the Kostka coefficients and the binomial coefficients that extends to the
q,t case. Below are only the tables through n=4, TEX,
postscript and PDF versions of these tables through n=5 are also available.
These coefficients were remarked to be q,t analogs of the binomial coefficients
in the paper Affine Hecke algebras and raising operators for Macdonald
polynomials by A. Kirillov and M. Noumi. When lambda is a hook
they were remarked to be a q,t analog of the falling factorial (but with
the wiggled Kostka coefficients and an additional formula) in the article
Identities
and Positivity Conjectures for Some Remarkable Operators in the Theory
of Symmetric Functions ( F. Bergeron, A. M. Garsia, M. Haiman and G.
Tesler ).
| n=2 |
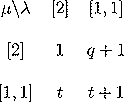
 |
| n=3 |
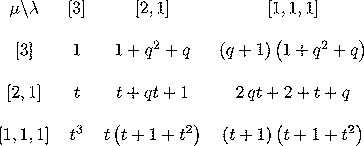
 |
| n=4 |
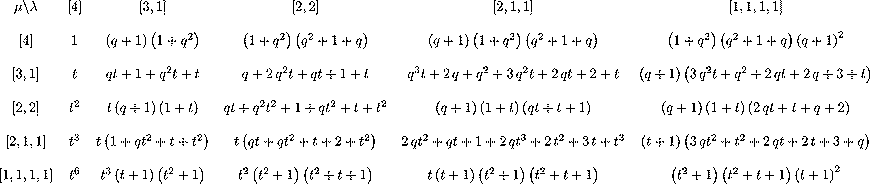
 |