| Professor
Mike Zabrocki Office: TEL 3046 Hours: Thursday 4-5:30pm phone: 416-736-2100 x33980 e-mail:  |
| Class
meets Thursday 6-9pm in VC 102 |
| Text : Number Theory by George Andrews |

Math 5020Fundamentals of Mathematics for Teachers |
| Description:
Number Theory and Combinatorics are branches of
mathematics in which theorems and problems are usually easy to state
but often difficult to prove or resolve. This course will deal with
topics in these two fundamental mathematical fields, including modular
arithmetic, linear and quadratic diophantine equations, continued
fractions, permutations and combinations, distributions and partitions,
recurrence relations,
generating functions, formal power series. The use of computers
for mathematical exploration will
be encouraged through the computer program Maple. The course will
cover material from 'Number Theory' by George Andrews and supplementary
material on generating functions and species. |
|
 |
| Course presentation
topics |
||
| Fermat's Little Theorem |
Kevin Smith |
Sept 29 |
| Wilson's Theorem |
Shirley Ting |
Oct 6 |
| card shuffling |
Pierre Lacoste |
Oct 20 |
| solving congruences |
Dorota Mazur |
Oct 27 |
| chinese remainder theorem |
Pauline Fu |
Nov 3 |
| multiplicative functions |
Mike Eden |
Nov 10 |
| Möbius inversion |
Samia Saleh | Nov 17 |
| primitive roots |
Jeff Irwin |
Nov 24 |
| distrib. primes &
Tchebychev's ineq |
Toni Katsinos & Carol Miron |
Dec 1 |
| quadratic reciprocity |
Melissa Giardina & Paul Attar |
Jan 5 |
| pseudo-primality testing Jacobi
and Legendre symbols |
Ada Tsui & Andrea Young |
Jan 12 |
| RSA and Digital Signatures |
Taravat Moshtagh |
Jan 19 |
| Sum of 4 squares theorem |
Keith Auyeung |
Jan 26 |
| Generating functions |
Anisoara Preda |
Feb 2 |
| Jacobi triple product identity |
Anna Yoon |
Feb 9 |
| Fermat's Last Theorem and A. Weil |
Margarita Panayotova |
Feb 16 |
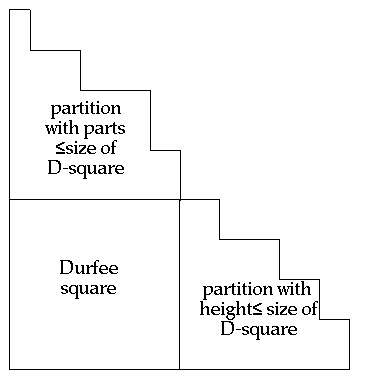
| Ferrer's diagrams and partition
ident. |
||
| partitions which fit in a
rectangle |
||
| Class
presentation |
20% |
| Un-exams
(4 x) |
10%+10%+15%+15% |
| Forum exercises | Fall
15%+Winter 15% |
| Sept 12 - Sect 1.1, 1.2, 2.1 |
| Sept 19 - Sect 2.2, 2.3 |
| Sept 26 - Sect 3.1, 3.2 |
| Oct 6 - Sect 3.3, 3.5, 4.1, 4.2 |
| Oct 20 - Sect 4.3 |
| Oct 27 - Sect 5.1, 5.2 |
| Nov 3 - Sect 5.3 |
| Nov 10 - Sect 6.1,6.2,6.3 |
| Nov 17 - Sect 6.4 |