Problem list
The problems that I assigned during the fall term are here.
I will continue to post homework problems that I am assigning here. You should be
doing as many of the problems that I assign as you can manage for practice (but you do
not need to spend the time writing them in full solution form like I am asking you to
do for the forum). We will
be taking more time this term to do problems in class too.
I mentioned in class my criterion for what I am looking for in these solutions:
(1) clear - no vague sentences that have multiple interpretations, no gaps in the
explanation, very direct and to the point
(2) complete - include all relevant details. If you are writing a solution to a counting
problem about cards, I want to see the connection between the description of what you
are counting and how you are creating a procedure to which you can apply the addition
and multiplication principle. This need only be one sentence, but if that sentence
is missing the solution is not complete. For other types of problems I am looking for
a logical sequence of arguments.
(3) short - this this a secondary criterion but it is extremely important that
you not ramble on.
I am not looking to see how you solved this problem, save that for your
own notes. What I am looking for is that you explain to me why what you said is true and
not a sentence more.
I need to be convinced of one thing only: beyond a shadow of a doubt, your solution is correct.
(Jan 5)
As I noted in the announcements I gave out a worksheet on
sequences and sets of objects. This worksheet is a list of examples of things
that are 'widgets' and I am asking you to calculate 'numbers of widgets.'
There are 25 problems on this worksheet and I recommend that
you do at least 1 of them. If you want a real challenge, try doing one of 21 through 25.
These last 5 problems are likely to lead to a lot of work.
(Jan 21)
On the latest worksheet that I gave out on the
17th you were asked to find the coefficient of q^n in an expression for a generating
function. If we again
assume that "a_i = the number of widgets of size i" then that expression represents
the number of some sort of combinatorial object. In the following problems I ask
you to give me a description of a set of objects such that the number of objects of
size n is equal to the coefficient of q^n.
For example:
the coefficient of q^n in A(q)^2 is
a_n a_0 + a_{n-1} a_1 + a_{n-2} a_2 + ... + a_1 a_{n-1} + a_0 a_n.
therefore A(q)^2 is the generating function for pairs consisting of a widget of size
r_1 and a widget of size r_2 such that r_1 + r_2 = n.
Alternatively, A(q)^2 is the generating function for the pairs consisting of two widgets where
the size of the pair is equal to sum of the sizes of the widgets.
The following is a list of some of the questions on that worksheet for which I would
like a "meaning" for. That is we assume that A(q) is the generating function for
the number of widgets of size n (that is if a_i = number of widgets of size i, then
A(q) = \sum_{i \geq 0} a_i q^i) and I would like you to find a description for the
generating functions below. Your forum posting should tell me what the coefficient of
q^n is (which is why I would like to go over those in class)
and also have a description of what this generating function represents.
A. 29,
B. 17,
C. 24,
D. 7,
E. 27
F. 20,
G. 19,
H. 23,
I. 14,
J. 22
K. 16,
L. 5,
M. 26,
N. 28,
O. 9
P. 15,
Q. 12,
R. 6,
S. 25,
T. 18
U. 4,
V. 10
(Jan 24) find a meaning for the generating function
1/(1-q A(q))
(Jan 24) If you stack
cannonballs in a pile with 1^2 cannonballs on the first level, 2^2 cannonballs on
the second level, 3^2 cannonballs on the third level, etc. How many
levels (greater than 1) do you need to have so that when the stack is
laid out flat that it can be made into a square?
(a) write an elliptic equation which describes the cannonball problem
(b) use elliptic equation addition to solve the problem (hint: (0,0)
and (1,1) should both be points on your curve and by adding them
together you will get a third)
(Feb 1) Show that (q+q^2)/(1-q)^3 = \sum_{n \geq 0} n^2 q^n and
(q+4 q^2 + q^3)/(1-q)^4 = \sum_{n \geq 0} n^3 q^n
(Feb 7) I am giving a worksheet out tonight
making a connection
between generating functions and combinatorial problems. The object of
this assignment will for you to explain to me (using the addition and
multiplication principle of generating functions) why a generating function represents
a given combinatorial description. I don't really care about the numerical
answer right now because we will concentrate on taking coefficients in generating
functions later, but what I am looking for is a good explanation of why the
generating function relates to the problem at hand.
W. 11a,
X. 11b,
Y. 11c,
Z. 11d,
AA. 6a,
BB. 6b,
CC. 6c,
DD. 6d,
EE. 7a,
FF. 7b,
GG. 7c,
HH. 7d,
II. 8a,
JJ. 8b,
KK. 8c,
LL. 8d,
MM. 8e,
NN. 9a,
OO. 9b,
PP. 9c,
QQ. 9d,
RR. 9e
(Feb 22) Exercises on taking coefficients in generating functions.
(Feb 29) SS. find a formula for
the Lucas numbers in terms of phi^n and phibar^n.
From Fibonacci generating function exercises
*TT. Fibonacci generating functions #1
*UU. Fibonacci generating functions #2
*VV. Fibonacci generating functions #3
*WW. Fibonacci generating functions #4
*XX. Fibonacci generating functions #5
*YY. Fibonacci generating functions #6
(March 11) I posted two worksheets on converting sets of partitions into
their generating functions. The first one is a
matching exercise.
The second is a
long list of sets of partitions
which I would like you to be able to give me a formula for their
generating function.
We will certainly need to talk about these when we get back
on March 21st. The idea is to take a description of a set of partitions and then
break that set into tuples or disjoint unions of smaller sets of partitions
where you know how to take the generating function.
In class we talked about for instance P_k(q) = the generating function for the
partitions with parts of size less than or equal to k. Then
P_k(q) = \product_{i=1}^k 1/(1-q^i)
O(q) = the generating function for partitions with odd parts only
O(q) = \product_{i \geq 0} 1/(1-q^{2i+1})
S(q) = the generating function for partitions with strict parts (that is, no two
parts are of the same size)
S(q) = \product_{i \geq 1} (1 + q^i)
If you do not understand these examples then there is no sense in proceeding
further because the problems ahead assume that you understand how to convert
a description for a set of partitions into a generating function. You should do ALL the
problems on the matching worksheet
and make sure that you understand those because
the next step is to be able to arrive at
the generating function from the
description yourself. If you would like to know the answers to that worksheet
before March 21, email me YOUR solutions and I will tell you which ones are correct.
Example 1: Partitions of n with parts which are multiples of 3.
Every partition of n with parts that are multiples of 3 can be described
as an infinite tuple ( x3, x6, x9, x12, ... ) where x_{3*i} = the number of parts
of the partition which are equal to 3i. Because we started with a
partition of n, \sum_{i >= 1} 3*i* x_{3*i} = n.
By the multiplication principle,
the generating function for this
set of partitions will be the product for each i >=1
of the generating functions for the partitions
of n with parts only of size 3*i.
There is exactly one partition of size
3*i*k for each k >= 0 using only parts of size 3*i, hence the generating function
for the partitions using only parts of size 3*i is 1/(1-q^{3*i}).
Therefore
the generating function for the partitions of n with parts which are
multiples of 3 is equal to \product_{i >=1} 1/(1-q^{3i}).
For some sets of partitions it is not obvious that one would want to decompose
the partition naturally into its parts. You may need to draw a few examples before
you see how to decompose the set.
Example 2: A Durfee square of size 3 and all odd parts.
First step is to draw some examples such as:
(3,3,3) or (3,3,3,1) or (5,3,3) or (9,7,7,3,3,3,1,1,1,1).
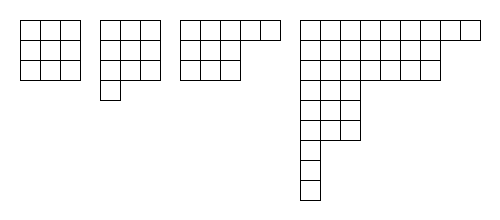As an exercise you should try to draw 5 more partitions that fall
into this set before you continue. If you draw 10 more then
hopefully you will see that there is a natural way of decomposing
these partitions. Click here to
see the rest of the solution to this problem. Remember, do not
click on this link UNTIL YOU HAVE DRAWN AT LEAST 5 MORE PARTITIONS
that fall into this set.
Below is the list of problems that I would like you to do for your
forum question. I picked out the ones that were (for the most part)
sets of partitions which are non-trivial to decompose. Please give them
some thought and ask me for help if you need it.
ZZ. 2,
AAA. 3,
BBB. 6,
CCC. 7,
DDD. 10,
EEE. 12,
FFF. 13,
GGG. 16,
HHH. 18,
III. 19,
JJJ. 21,
KKK. 22,
LLL. 23,
MMM. 24,
NNN. 25,
OOO. 27,
PPP. 28,
QQQ. 29,
RRR. 30,
SSS. 31,
TTT. 32
below is the list of problems that I would like you to post. The conversion
of the letter to the problem is in the paragraphs above.
| Abbasi |
Nader |
A |
W |
ZZ |
| Aniceto |
Paul |
B |
X |
AAA |
| Bhatti |
Abbas |
C |
Y |
BBB |
| Constantin |
Violeta |
D |
Z |
SS |
| Cuda |
Michael |
E |
AA |
CCC |
| Curic |
Vidak |
F |
BB |
DDD |
| Cuschieri |
Pierre |
G |
CC |
EEE |
| Filizola |
Regiane |
H |
DD |
FFF |
| Glavine |
Vincent |
I |
EE |
GGG |
| Goyat |
Laxmi |
J |
FF |
HHH |
| Heron |
Radcliffe |
K |
GG |
III |
| Lim |
Louis |
L |
HH |
JJJ |
| Malltezi |
Etleva |
M |
II |
KKK |
| Nelsons |
Betty-Ann |
N |
JJ |
LLL |
| Nwosu |
Kelechi |
O |
KK |
MMM |
| Puzniak |
Malgorzata |
P |
LL |
NNN |
| Richer |
Danielle |
Q |
MM |
OOO |
| Rieger |
Margaret |
R |
NN |
PPP |
| Roberts |
Catherine |
S |
OO |
QQQ |
| Soster |
Mario |
T |
PP |
RRR |
| Tauts |
Thomas |
U |
QQ |
SSS |
| Woodcock |
Jennifer |
V |
RR |
TTT |
Back to the web page for Math 5020.
The problems that I assigned during the fall term are here.