Course description:
Extended exploration of elementary problems leading to conjectures, partial
solutions, revisions, and convincing reasoning, and hence to proofs.
Emphasis on problem solving, reasoning, and proving. Regular participation
is required. Prerequisite: 12U Advanced Functions (MHF4U) or Advanced
Functions and Introductory Calculus (MCB4U). NCR note: Not open to any
student who is taking or has passed a MATH course at the 3000 level or higher.
Most High School mathematics problems are solved using algorithmic methods or
via reference to model solutions. One purpose of this course is to enable
students to develop the confidence and ability to attack richer and more
demanding problems. The attempt to check work and to explain one’s discoveries
to others leads naturally to the need for explanation. Learning how to present
convincing reasoning — or proof — is one of the course outcomes.
With an emphasis on communication/convincing argument, there is a critical
contribution to be made by: group work, reading a proposed 'proof' including
other student's work, presenting and discussing as a whole class. There is also
value in working through several different approaches to solve a problem, and
taking the time to understand an alternative approach offered by a peer in the
class. Doing mathematics well includes talking and listening to mathematics
and there will be assignments that require collaborative work with another
student in the class, as well as support for forming study groups.
The main goal of this course is to develop skills that lead to understanding
and communicating a convincing argument. Support will be given for proof
presentation, especially for the kinds of proofs that students are expected
to produce in their second year and higher level courses. This includes
inductions, and arguments with counting and with inequalities. Formal proof
writing exercises will be introduced in the second half of the course, once
problem solving and informal justification skills reach an acceptable level.
Class and tutorial attendance is mandatory and active participation is
expected of all students.
Course references:
The course textbook is
Martin Liebeck, A Concise Introduction to Pure Mathematics, Third Edition.
It is recommended, but not required.
Other useful references are
John Mason, Leone Burton, Kaye Stacey, Thinking Mathematically, Second Edition.
This book gives an approach to problem solving and the problem solving experience.
It is also a source for rich and varied problems.
G. Polya, How to Solve It: A New Aspect of Mathematical Method.
Course components:
The evaluation will be based on the following criteria
Participation
|
based
on attendance and in class assignments
|
|
Assignments
|
roughly
one every 3-4 weeks
|
25%
|
Quizzes
|
6
total, 3 per term, best 2 from each term
|
30%
|
Final
Examination
|
Winter
exam period
|
45%
|
Do your own work. Don't look for a solution on the web or take one
from another student's work unless you already have found your own
solution and intend to review another to make a comparison. Work that
is not original will be graded accordingly. Presenting someone else's
work as your own without proper citation is academic dishonesty. You must
cite any internet sources which you have consulted.
I recommend that you look carefully at the
York University Academic Integrity Tutorial.
Participation: You are expected to show your commitment to this course and
your fellow students by sharing your mathematical knowledge of the material.
Attendance at the weekly classes and the tutorials is obligatory and you
will lose 2 points from your course grade for each class or tutorial that
you miss each term. Sometimes attendance at the weekly classes will be
measured by a short in class assignment. Non participation in these
assignments will result in a lowering of your participation grade.
Note that participation is not a percentage of your grade, but
non-participation and attendance can lower your overall score.
Assignments: There will be roughly one assignment 3-4 weeks.
Most assignments will require explanation beyond a simple one or
two word/numerical answer. It is good practice to RECOPY THE QUESTION
EVERY SINGLE TIME when you do the assignment. This makes it possible
to understand what the assignment when it is handed back to you and
it attempts to reduce the error of answering a different question
than is on the assignment. Full credit is given to papers which
demonstrate deep understanding of the problem by providing multiple
solutions and considers variations based on the original question
when this is appropriate. Your assignment should include complete
sentences and explanations and not just a few equations or numbers.
A solution will not receive full credit unless you explain what your
answer represents and where it came from. You may discuss the homework
with other students in the class, but please write your own solutions.
You should prepare your assignments in LaTeX and hand them in on the online
Moodle. LaTeX is a program that was designed for writing mathematics. Information
about how to do this is provided
on this page and we will discuss it more in class.
Note: Late assignments will be penalized by 10% per day. This will
apply to any homework handed in after the class time in which it is
due. In addition, assignments which are handed in late are unlikely
to be marked in a timely manner.
Here is a breakdown of some aspects that I plan to evaluate your solutions. Before you
hand in your assignment, I recommend that you read it though carefully and try to address the points
from this list.:
(1) The discussion begins with an explanation of the problem
(2) The explanation should convince the reader that the meaning of the question is understood (e.g. small examples, a clearly labeled table of data, and/or a discussion of the meaning of the question)
(3) diagrams, tables or images that are drawn to aid the reader in understanding the problem are well labeled and explained
(4) Clear statements are made of conjectures that are believed to be true
(5) Explanations of why those conjectures are true are included
(6) An explanation of how the problem solving process proceeded is clear from the explanation
(7) The entries consist of writing which is clear and grammatically correct
(8) A conclusion about the solution to the problem is reached
Note that to receive full credit you must go beyond simply solving the problem as posed. Learn to think of your solutions as a starting point.
Quizzes and Final Examination: There will be 3 quizzes per term (dates listed below). A final examination will be scheduled for the April exam period and the date announced in late-February/early March.
Announcements:
(September 5, 2017) Welcome! The first day of classes is Tuesday, September 12
and the class will be held in the Life Sciences Building room 107.
Instructions about the tutorials (which are scheduled for Wednesdays) will
be given on the first day of class. They will meet for the first time
on Wednesday, September 20.
(Sept 12, 2017) For next time I would like you to:
(1) read carefully and be aware of the
online academic integrity tutorial
(2) learn to use
LaTeX and
write a summary of the problem
we discussed today in class. I will ask you to hand it in on Moodle.
(3) watch the following
video on telescoping sums.
(Sept 12, 2017) While I was in class I was hoping to upload a picture and show
you how to insert it in your document, but I couldn't find how to upload a picture
onto ShareLaTeX. It turns out that I was missing it because it is subtle and
it looks like this:
You might want then to include that image in your file with the
LaTeX command like
\includegraphics[width=3in]{image.jpg}.
(Sept 15, 2017) I adjusted the schedule a bit and corrected the dates for the
tutorials. They will meet every other week and both tutorials will meet the
same day. There will be 12 meetings of the tutorials and during 6 of those
we will have the quizzes.
(Oct 2, 2017) You will have a quiz tomorrow in the tutorial. You will need
to be able to prove a
sum formula using
telescoping sums. You will also need to justify a some simple logical statements
or provide a counter-example.
(Oct 2, 2017) I read your homework assignments and gave you some feedback.
Everyone who handed in a latex assignment got full credit, but future assignments
will be evaluated more on content.
Some general comments about what I saw:
- Reread your sentences and make sure they are as simple and clear to another
reader as you can make them
- Don't ramble on. Your final solution should be short and direct.
We don't need to know your whole process about how you discovered the answer,
just a clear and short explanation of why it is true
- Make sure that you define all notation and abbreviations that you use
- Don't use shorthand notation when you write unless it makes the text more readable
- Do not begin a sentence with a symbol
(Oct 29, 2017) I posted
a pdf file with some problems
to act as practice for
the quiz this week.
(Jan 8, 2018) Welcome back. I am going to have to adjust my office hours for
this term. I will not be available this week, but I will start them the week
of the 15th.
(Jan 23, 2018) Just an FYI, a version of the worksheet on binomial identities
that I had on the website earlier today had a few typos. They have been corrected
and a version was added that indicates the date and time it was updated (at the bottom left).
You should use this worksheet to practice writing expressions in summation
notation as well as proving binomial identities by induction.
(Jan 23, 2018) Do you want to see the
Sierpinski triangle
in
Pascal's triangle?
Try the command that I used in class in
the Sage cell server:
sum([point2d((n,k)) for n in range(128) for k in range(n+1) if mod(binomial(n,k),2)==1])
The command draws all of the points $(n,k)$ for $0 \leq n \leq 127$ and
$0 \leq k \leq n$ such that ${n \choose k}$ is odd.
(March 12, 2018) The class will go on as scheduled and I will record the
lectures. Tutorials are cancelled until the strike is over.
(March 20, 2018) The quiz for next week is cancelled and will be held on the
last day of class (April 3) instead. This will be the case even if the strike
is resolved and tutorials begin again next week.
Homework #7 is an optional assignment.
Hand it in on the moodle before April 11.
(March 27, 2018) I will be holding a quiz next week. I'll weight it so
that it is to your advantage to take it (either I transfer the weight to
the final if the strike continues, or I will count it if it improves your
grade).
We had a guest come into class just before it started to make a short
announcement about an information session about internships. This meeting
is to be held tomorrow at 4pm in Founders 152. If you are interested
please email
actsciyorku@gmail.com
One of the problems on the practice had two parts to it. The first part
we were able to argue that there must be at least 3 points in a
square with area 1, but the second part we needed to explain why
the largest triangle
that fits inside of a square with area 1 has area 1/2. None of this
made it into the video.
(April 16, 2018) I graded the quizzes, but not the two homework assignments yet.
Since I won't be able to cover the quiz in class let me make a few comments here:
1. The first question was to find and prove a formula for $f(n) = \sum_{r=1}^n \frac{1}{(4r+1)(4r-3)}$.
It really separated the people who understood summation notation from
those who didn't.
That means you first have to understand what that expression represents.
It
says that the variable $r$ varies from 1 to $n$ and you add up all of the expressions
when you plug in the values of $r$. That means if $n=1$, then $r$ varies from
$1$ to $1$ (that means there is one term) and $f(1) = \frac{1}{(4\cdot 1+1)(4\cdot1-3)} = 1/5$.
If $n=2$ then there are two terms in the sum, $f(2) = \frac{1}{(4\cdot 1+1)(4\cdot1-3)} + \frac{1}{(4\cdot 2+1)(4\cdot2-3)} =
2/9$. If $n=3$, $f(3) = \frac{1}{(4\cdot 1+1)(4\cdot1-3)} + \frac{1}{(4\cdot 2+1)(4\cdot2-3)}
+ \frac{1}{(4\cdot 3+1)(4\cdot3-3)}= \frac{3}{13}$ and
$f(4) = \frac{1}{(4\cdot 1+1)(4\cdot1-3)} + \frac{1}{(4\cdot 2+1)(4\cdot2-3)}
+ \frac{1}{(4\cdot 3+1)(4\cdot3-3)} + + \frac{1}{(4\cdot 4+1)(4\cdot4-3)} = \frac{4}{17}$ .
What was really great was it seemed that all the people that were able to guess
at the formula for $f(n)$ almost all also gave a clear and complete proof by induction.
2. The second problem no one gave a complete answer (although there were many that were close).
It was almost the same as the homework question so I was expecting more to get this
correct. You were asked to find a polynomial $p(x)$ such that $p(1)=2, p(2)=11$ and $p(3)=28$
and $p(k)$ for $k\geq 1$ is the value on the ray of the diagram traveling East from the 2 in the picture
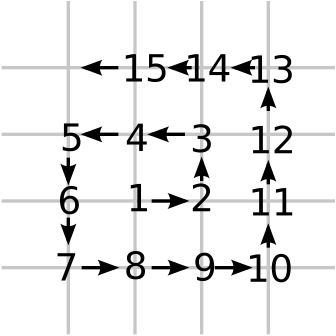
The hard way to do this
is to set up system of linear equations and solve. Go back and watch the video
from March 20 to see the easy way of writing down a polynomial. You were then
asked to tell me what $p(0), p(-1), p(-2),$ etc. was equal to. Almost everyone
assumes that $p(0)=1$, $p(-1) = 6$ and $p(-2)=19$ (BUT IT IS NOT THE CASE!).

